Sistemas de ecuaciones: método de reducción
- Detalles
- Categoría: 1º Bachillerato
- Publicado el Domingo, 05 Febrero 2012 12:22
- Escrito por Mariano Herrero
Estudiamos uno de los mejores métodos para para resolver sistemas:
- sistemas de dos ecuaciones con dos incógnitas
- sistemas de tres ecuaciones con tres incógnitas
Sistemas lineales de dos ecuaciones con dos incógnitas
Método de reducción: Consiste en eliminar una de las incógnitas mediante una combinación lineal (multiplicar las ecuaciones por un número para que la incógnita a eliminar tenga el mismo coeficiente en ambas ecuaciones) de las ecuaciones, obteniendo una ecuación con una sola incógnita. Después se repite con la otra incógnita.
Ejemplo 1: Resolver el siguiente sistema: ![]()
Eliminamos la incógnita x: como en la 1ª ecuación el coeficiente de la x es 2 y en la 2ª es 1, multiplicamos ésta por − 2 
quedando una ecuación con una incógnita, que despejando tenemos (− 9 que está multiplicando a la y, pasa dividiendo al otro miembro): y = −9/(−9) = 1
De igual forma eliminamos la y: como en la 1ª ecuación el coeficiente de la y es −1 y en la 2ª es 4, multiplicamos la 1ª por 4: 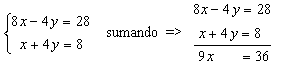
como antes, queda una ecuación con una incógnita, que despejando tenemos (9 que está multiplicando a la x, pasa dividiendo al otro miembro): x = 36/9 = 4
Solución: x = 4; y = 1
Método de reducción –sustitución
En la práctica se usa el método de reducción –sustitución (como la propia palabra indica es una mezcla de ambos métodos). Primero se reduce una incógnita como se ha expuesto anteriormente y luego se sustituye este resultado en la otra.
Ejemplo 2: Resolver el siguiente sistema: ![]()
Eliminamos la incógnita y, ya que tiene coeficientes opuestos, que sumando conseguimos: 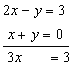
así obtenemos una ecuación con una incógnita, que despejando tenemos x = 3/3 = 1
sustituyendo éste valor de x en la 2ª ecuación resulta: 1 + y = 0 => pasando el 1 del primer miembro al 2º con signo “ − “ obtenemos y = − 1
Solución: x = 1; y = −1
Sistemas lineales de tres ecuaciones con tres incógnitas
Aplicamos el método de reducción: Tomamos dos ecuaciones cualesquiera y eliminamos una incógnita, resultando una ecuación con dos incógnitas; ahora tomamos la que queda con una cualquiera de las dos tomadas anteriormente y eliminamos la misma incógnita que en el caso anterior, resultando otra ecuación con las dos incógnitas anteriores. De esta forma hemos reducidos el sistema a dos ecuaciones con dos incógnitas.
Se deben seguir las pautas indicadas, pues en caso contrario llegaremos a una igualdad como CERO = CERO, nos liaremos y y no resolveremos el sistema.
Ejemplo 3: Resolver el siguiente sistema: 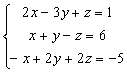
Tomamos las dos primeras ecuaciones y eliminamos la incógnita x: como en la 1ª ecuación el coeficiente de la x es 2 y en la 2ª es 1, multiplicamos ésta por −2: 
Tomamos la ecuación que queda (la 3ª) con una cualquiera de las dos tomadas anteriormente (elegimos la 2ª): 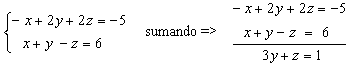
Así conseguimos el sistema equivalente (segunda ecuación del sistema inicial más estas dos ecuaciones donde se ha reducido la x): 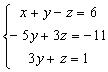
Elegimos estas dos últimas ecuaciones, y de nuevo por reducción, eliminamos la z; como en la 1ª ecuación el coeficiente de la z es 3 y en la 2ª es 1, multiplicamos ésta por − 3: 
queda una ecuación con una incógnita, que despejando tenemos y = −14/(−14) = 1
sustituyendo éste valor de y en la 2ª ecuación resulta: 3·1 + z = 1 => 3 + z = 1
pasando el 3 del primer miembro al 2º con signo “ − “ queda z =1− 3 = − 2
Con estos valores de y = 1 y z = − 2 sustituimos en la 2ª ecuación del sistema inicial y se obtiene: x + 1 – (– 2) = 6 => x + 1 + 2 = 6 => x + 3 = 6 => x = 3
Solución: x = 3; y = 1; z = − 2
