Ejemplo2 programación lineal PAEG junio 2010
- Detalles
- Categoría: 2º Bachillerato
- Publicado el Miércoles, 12 Octubre 2011 16:52
- Escrito por Mariano Herrero
Ejemplo 2: Una fábrica de ordenadores va a lanzar al mercado dos nuevos modelos (uno básico y otro de lujo). El coste de fabricación del modelo básico es de 300 € y el del modelo de lujo 1000 €, disponiendo para esta operación del lanzamiento de 28000 €. Para evitar riesgos, de momento se cree conveniente lanzar al menos el doble de ordenadores del modelo básico que del modelo de lujo y, en todo caso, no fabricar más de 50 ordenadores del básico. Además se quiere fabricar no menos de 10 ordenadores de lujo.
a) Representa la región factible.
b) ¿Cuántos ordenadores debe fabricar si quiere maximizar el número total de ordenadores fabricados?
c) Si se fabrica el máximo número de ordenadores posibles, ¿agota el presupuesto disponible? Universidad Castilla La Mancha PAEG junio 2010
Sea x el número de ordenadores tipo básico e y los de tipo de lujo
Función objetivo es: el número total de ordenadores es f(x, y) = x + y
Restricciones: 300x + 1000y ≤ 28000 => 3x +10y ≤ 280 (coste a 300 el básico + 1000 el de lujo)
2x ≥ y (como mínimo el doble de ordenadores del modelo básico que de lujo)
x ≤ 50 (menor o igual de 50 ordenadores del básico)
y ≥ 10 (10 o ḿas ordenadores de lujo)
El recinto de soluciones es el formado por las cuatro rectas correspondientes a las inecuaciones de las restricciones: Debemos conocer al menos dos puntos de cada recta, que se determinan dando los valores que queramos a una de las variables :
Dos puntos de la recta 3x +10y = 280 son (0, 28) y (20, 22)
La recta y = 2x pasa por los puntos (0, 0) y (10, 20). La recta x = 50 es vertical y la y = 10 es horizontal.
Si prolongamos la unión de cada uno de los pares de puntos correspondiente a cada recta tenemos la representación gráfica de susodichas rectas. La región factible es la representada en la gráfica de color morado formada por el cuadrilátero ABCD.
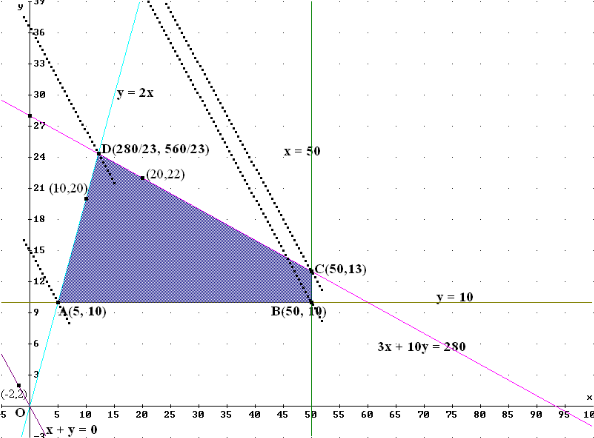
Las coordenadas de los vértices A, B, C, D se obtienen resolviendo el sistema de las dos rectas que pasan por cada vértice. El punto A(5, 10) es la solución del sistema {y = 2x e y = 10}, el punto C (50,13) resolviendo el sistema {3x +10y = 280 e x = 50} y el D(280/23, 560/23) el resultado del sistema {3x +10y = 280 e y = 2x}.
Método gráfico: La recta de nivel tiene por ecuación x + y = 0; si trazamos rectas paralelas por los puntos A, B, C y D tenemos las rectas punteadas.
a) Como hemos de maximizar, la solución es el punto C(50, 13) pues por él, pasa la recta que corta al eje Y con mayor ordenada (en la gráfica no llega a cortar, pero se ve que es dicha recta, ya que para que corte, la escala de ordenadas debe alcanzar 94 y la gráfica se vería muy pequeña).
La solución es: 50 ordenadores de tipo básico y 13 de tipo lujo
b) El máximo número de ordenadores es : F(50, 13) = 50 + 13 = 63.
c) Los 50 ordenadores de tipo básico cuestan: 50·300 = 15000 € y los 13 de tipo lujo cuestan : 13·1000 = 13000 € , lo que hace un total de 28000 €. Luego agota el presupuesto.
Método analítico: Sabemos que la solución óptima está en los vértices del recinto de soluciones (en el cuadrilátero ABCD); veamos el número de ordenadores totales sustituyendo en cada vértice la función objetivo:
F(A) = F(5, 10) = 5 + 10 = 15. F(B) = F(50, 10) =50 + 10 = 60
F(C) = F(50, 13) = 63. F(D) = F(280/23, 560/23) = 280/23 + 560/23 = 840/23
El mayor es F(C) = 63 como ya habíamos visto antes.


