Método de Gauss
- Detalles
- Categoría: 2º Bachillerato
- Publicado el Jueves, 15 Marzo 2012 22:19
- Escrito por Mariano Herrero
Consiste en sustituir el sistema dado por otro equivalente (que tenga las mismas soluciones), tras sucesivas transformaciones, para conseguir un sistema triangular escalonado. El proceso consiste en hacer CEROS por debajo de la diagonal principal.
Se obtienen sistemas equivalentes:
- Si se intercambian entre sí dos ecuaciones. Si se multiplica (divide) una ecuación por un número distinto de 0.
- Si se hace una combinación lineal de ecuaciones (se suma o resta a una ecuación otra u otras multiplicada por un número).
- Se pueden suprimir las ecuaciones combinación lineal de otras.
Resolución de sistemas por Gauss
- Se toma la matriz de coeficientes y separada con una línea vertical, la matriz columna de términos independientes (matriz ampliada).
- Si en alguna ecuación falta alguna incógnita, su coeficiente correspondiente es 0.
- El primer elemento de la primera ecuación (fila) es conveniente que sea 1, aunque no necesario; para ello se intercambian ecuaciones.
- Se hacen trasformaciones por filas (aunque también se pueden hacer por columnas) mediante combinaciones lineales. Se puede hacer varias trasformaciones a la vez.
Por regla general en la diagonal principal (que parte del primer elemento de la primera ecuación (fila)) sobre todo cuando depende de algún parámetro no puede haber CEROS, ya que podemos multiplicar por CERO sin enterarnos; si esto ocurre se deben intercambiar ecuaciones (filas) o incluso columnas (en este caso se intercambian incógnitas).
Si se llega a una situación (0 0 0... 0 | 0), es decir una fila con todos sus elementos CEROS, se puede suprimir esta ecuación (fila).
Si se llega a una situación (0 0 0... 0 | a ≠ 0), significa una situación absurda (el sistema es incompatible, no tiene solución; (rango (A) ≠ rango (A*)); rango (A) es el rango de la matriz de coeficientes, mientras que rango (A*) es el rango de la matriz ampliada.
Si el sistema depende de un parámetro, es conveniente arrinconarlo en el extremo inferior derecho para facilitar las trasformaciones.
Si el sistema es compatible indeterminado (S.C.I.), entonces el sistema tiene infinitas soluciones; las incógnitas dependerán de uno o más parámetros. Este número de parámetros es la diferencia entre número de incógnitas y rango de la matriz de coeficientes (número de incógnitas y número de ecuaciones linealmente independientes).
Ejemplo: Resolver el sistema 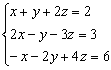
La matriz de coeficientes es:  y la ampliada:
y la ampliada: 
Nomenclatura operatoria entre filas y columnas
F1, F2 , F3 significa fila 1, 2, 3 respectivamente. Igualmente C1, C2 , C3significa columna 1, 2, 3
F1 <---> F2 se intercambian la fila 1 por la fila 2. De igual modo C1 <---> C3 se intercambian la columna 1 por columna 3.
La nomenclatura de la trasformación se debe poner a la altura de la fila trasformada, apareciendo esta en primer lugar.
F3 + F1 significa que se hace la trasformación sobre la fila 3, cuyo resultado es la suma de la fila 3 con la fila 1.
3F1 – 2F2, la trasformación se hace sobre la fila 1 que se coloca a la altura de esta fila; el resultado es la diferencia del producto de la fila 1 multiplicada por 3 y la fila 2 multiplicada por 2.
Aplicándolo al ejercicio, en primer lugar buscamos CEROS en los elementos a21 y a31, que hacemos primero uno y luego el otro (no importa el orden) o los dos simultáneamente. En este ejercicio hacemos dos trasformaciones a la vez.

Para hacer CERO a21: Hacemos la trasformación sobre F2 (fila 2); como a11 = 1 y a21 = 2, para conseguir CERO a21, a la F2 (fila 2) restamos F1 (fila 1) multiplicada por 2: F2 – 2F1 que ubicamos a la altura de la fila 2 (primero F2)
F2 – 2F1= (2 –1 – 3 3) – 2 (1 1 2 2 ) = (2 –1 – 3 3) – (2 2 4 4 ) = (0 – 3 –7 –1) => elementos de la fila 2
P.ara hacer CERO a31: Hacemos la trasformación sobre F3 (fila 3); puesto que a11 = 1 y a31 = –1, para conseguir CERO a31, a la F3 (fila 3) sumamos F1 (fila 1): F3 + F1 colocamos a la altura de la fila 3 (en primer lugar F3).
Por último para hacer CERO a32 , necesariamente la combinación lineal ha de ser con la fila 2, pues de otra forma perdemos parte del trabajo ya realizado.
Debemos hacer la trasformación sobre F3 (fila 3); como a22 = – 3 y a32 = –1, para conseguir CERO a32 , a la F3 (fila 3) la multiplicamos por 3 y restamos F2 (fila 2): 3F3 – F2 que hemos de situar a la altura de la fila 3.
Entonces el sistema escalonado equivalente es: 
Ahora utilizamos el método de sustitución "hacia atrás", comenzando por la tercera ecuación (despejamos la z) y subiendo hasta la primera.
De la 3ª ecuación: 25z = 25 => (25 que está multiplicando pasa dividiendo) z = 25/25 => z = 1
Entrando en la 2ª ecuación con z = 1 => – 3y –7(1) = –1 => – 3y = –1 + 7 = 6 => y = 6/(–3) => y = – 2
Por último entrando en la 1ª ecuación con z = 1 e y = – 2 => x + (–2) +2·1 = 2 => x = 2 + 2 – 2 = 2
Por tanto la solución es: x = 2; y = – 2; z = 1


