Sistemas de 3 ecuaciones y 4 incógnitas

• 
• 

Detalles

Categoría: 1º Bachillerato

Publicado el Jueves, 10 Enero 2013 20:44

Escrito por Mariano Herrero

Resolver el sistema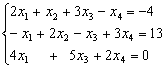

Nos topamos con un sistema de 3 ecuaciones y 4 incógnitas. Se puede resolver como se indica en el tema correspondiente (más incógnitas que ecuaciones), considerando la incógnita x₄ como dato, traspasándola al segundo miembro y resolviendo el sistema de 3 ecuaciones con 3 incógnitas 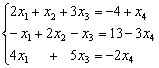       por los métodos ya conocidos.

Una vez resuelto, a la incógnita x₄  la hacemos igual a t.; las incógnitas  x₁, x₂, x₃, x₄ en general dependerán del parámetro t.
Este sistema de 3 ecuaciones u otros similares con más ecuaciones o incógnitas se obtienen mejores resultados por el método de Gauss.

Para ello localizamos CEROS por debajo de la diagonal principal, dos en la primera columna y uno en la segunda, mediante las trasformaciones permitidas que se indican en cada caso:

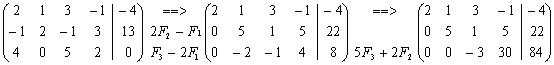
==> y el sistema equivalente queda: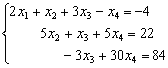

Las tres ecuaciones son independientes, por lo que según las indicaciones del Tma. de Rouché-Frobenius  el sistema es compatible indeterminado con un grado de libertad (4 ecuaciones – 3 ecuaciones linealmente independientes) y las incógnitas dependerán de un parámetro t; a la cuarta incógnita x₄ (puede ser cualquiera) la igualamos a t => x₄ = t

Para determinar las soluciones, por sustitución hacia “arriba”, despejamos x₃ de la 3ª ecuación: x₃ = (30x₄ –84)/3 = 10x₄ –28 = 10t –28
Con este valor entramos en la 2ª ecuación: 5x₂ + (10t –28) + 5t = 22 => 5x₂ + 15t = 50 => x₂ = (50 –15t)/5 = 10 – 3t
Por último sustituyendo en la 1ª: 2x₁ + (10– 3t) + 3(10t –28) – t = – 4 => 2x₁ + 10 – 3t + 30t – 84 = – 4 => 2x₁ +26t = 70 => x₁ = (70 – 26t)/2 = 35 – 13t

Así pues la solución: x₁ = 35 – 13t; x₂ = 10 – 3t; x₃ = 10t –28; x₄ = t

Asignando valores a t  tenemos las infinitas soluciones. Así si  t = 3 => x₁ = – 4; x₂ = 1; x₃ = 2; x₄ = 3

 

• < Previo
• Siguiente >