Sistemas de ecuaciones: método de sustitución
- Detalles
- Categoría: 1º Bachillerato
- Publicado el Sábado, 28 Enero 2012 17:50
- Escrito por Mariano Herrero
Vamos a utilizar este modo para resolver:
- sistemas de dos ecuaciones con dos incógnitas
- sistemas de tres ecuaciones con tres incógnitas.
También se estudian otros métodos como el de reducción de incógnitas, de Gauss o de la escalera o Cramer por determinantes o matricialmente (hallando la matriz inversa).
Sistemas de dos ecuaciones con dos incógnitas (sistemas de 2x2)
Método de sustitución: Consiste en despejar una de las incógnitas (alguna, si hay, que tenga coeficiente unidad; si no hay, aquella que tenga el coeficiente más pequeño) de una de las ecuaciones y con ese valor se sustituye en la otra. De esta forma queda un sistema de una ecuación con una incógnita.
El hecho de despejar una incógnita con coeficiente unidad significa, que al despejar dicha incógnita, ésta no tiene denominador, lo que simplifica las operaciones. Cualquier otro coeficiente implica que haya denominador.
A veces en alguna ecuación ya nos dan una incógnita despejada o incluso su valor; en estos casos simplemente la reemplazamos en la otra ecuación. (más ejercicios resueltos con estos casos y otros peculiares)
Ejemplo 1: Resolver el siguiente sistema: ![]()
La incógnita x de la primera tiene coeficiente 1, por consiguiente despejamos y queda: x = 5 + 3y
sustituyendo este valor de x en la segunda ecuación: 2(5 + 3y) + y = 3
quitando paréntesis: 10 + 6y + y = 3
pasando 10, que está sumando, al segundo miembro restando: 6y + y = 3 – 10
haciendo operaciones en ambos miembros: 7y = – 7
Despejando la y (el 7 que está multiplicando pasa dividiendo) y = –7/7 = –1
Con este valor de y entramos en la ecuación despejada anteriormente: x = 5 + 3y = 5 + 3·(–1) = 5 – 3 = 2
Así pues la solución es: x = 2; y = – 1
Ejemplo 2: Resolver el siguiente sistema: ![]()
Como no hay ninguna incógnita con coeficiente unidad, despejamos el coeficiente más pequeño: la x de la primera ecuación quedando ![]()
sustituyendo este valor de x en la segunda ecuación: ![]()
quitando denominador (el denominador “2” multiplica a todo lo demás menos a su numerador) y paréntesis (el “3” multiplica a cada uno de los sumandos del numerador): 36 + 9y + 8y = 2
pasando 36, que está sumando, al segundo miembro restando: 9y + 8y = 2 – 36
haciendo operaciones en ambos miembros: 17y = – 34
Despejando la y (el 17 que está multiplicando pasa dividiendo) y = –34/17 = –2
Con este valor de y entramos en la ecuación despejada anteriormente: ![]()
Por tanto la solución del sistema es: x = 3; y = – 2
Sistemas de tres ecuaciones con tres incógnitas (sistemas de 3x3)
Método de sustitución: Despejamos una incógnita (alguna, si hay, que tenga coeficiente unidad) de cualquiera de las ecuaciones; sustituimos el valor de esa incógnita en las otras dos ecuaciones y reordenamos términos, quedando un sistema de dos ecuaciones con dos incógnitas.
Observamos el sistema por si alguna ecuación tuviera despejada una de sus incógnitas; si ocurre nos han hecho parte del trabajo y la reemplazamos en las otras dos, formando un sistema de dos ecuaciones con dos incógnitas en la que ya no existe la incógnita despejada. Si al reemplazar en las otras dos ecuaciones no existe dicha incógnita, tomamos la ecuación tal como está. Estas circunstancias se estudian con ejemplos.
Ejemplo: Resolver el siguiente sistema: 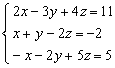
Despejamos x de la 2ª ecuación: x = 2z – y – 2
Sustituyendo el valor de x en las otras dos, resulta un sistema de dos ecuaciones con dos incógnitas ![]()
Quitando paréntesis y ordenando se obtiene: ![]() => y =3z – 3
=> y =3z – 3
Entrando con el valor de y en la 1ª ecuación: –5(3z – 3) + 8z = 15 => –15z +15 + 8z = 15 => z = 0
Sustituyendo (con z = 0) en y = 3z – 3 => y = 3·0 –3 = –3
Puesto que x = 2z – y – 2 => x = 2·0 –(–3) – 2 = 1. Solución: x = 1; y = –3; z = 0
Casos Particulares:
A veces en el trascurso de la resolución de un sistema nos encontramos con algunos inconvenientes, se atasca el ejercicio, y no sabemos resolver:
- Si encontramos una ecuación con 0x = 0, 0y = 0, 0z = 0, en general el sistema es indeterminado (tiene infinitas soluciones).
- Si encontramos una ecuación con 0x = a, a ≠0;, 0y = b, b ≠0;, 0z = c, c ≠0, (por ejemplo 0x = 7) el sistema es incompatible (NO hay solución).
En esta dirección se encuentra un ejercicio de cada caso.
Para nivel superior (los más aventajados) se puede estudiar la compatibilidad o incompatibilidad de sistemas y su resolución por otros métodos.


